后缀树组学习笔记(Suffix Array)

简介

后缀数组(Suffix Array)，主要是两个数组： $sa$ 与 $rk$ .

我们约定，后缀 $i$ 表示从 $i$ 开始的后缀。字符串下标从 $1$ 开始。

其中， $sa[i]$ 代表所有后缀中，第 $i$ 小的后缀的编号。
$rk[i]$ 代表后缀 $i$ 从小到大的排名。

有： $sa[rk[i]] = i$ ， $rk[sa[i]] = i$ .

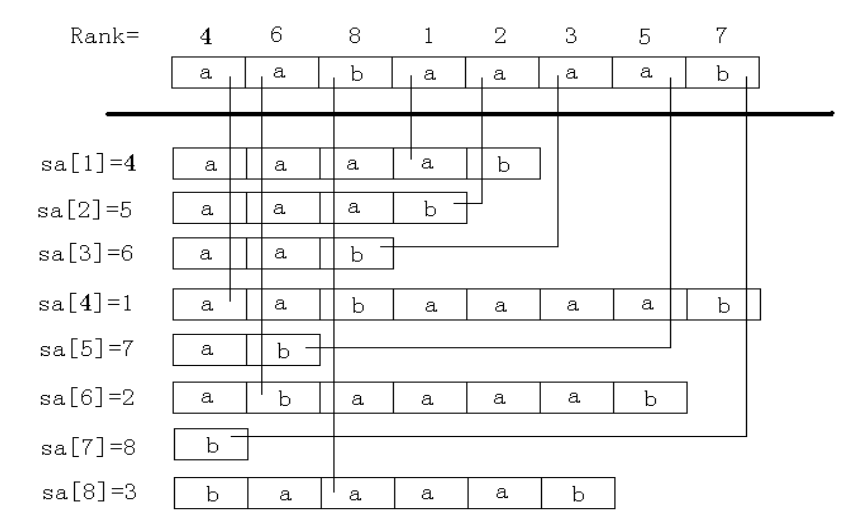
上图是一个后缀数组的例子。

可以发现，对于一个字符串，其所有后缀排序后，因为长度互不相同，得到的大小序列是唯一的。

求法

一个显然的求法，就是遍历所有后缀，扔进去排序，时间复杂度 $O(n^2 \log n)$ ，缺乏实用性。

在 OI 中，常常使用的是基于倍增和基数排序的求法，可以做到 $O(n \log n)$ 的时间复杂度。

利用倍增思想，假设我们已经知道长度为 $w$ 的字符串的 $rk$ 数组，现在要求出长度为 $2w$ 的字符串的 $rk$ 数组。

具体地， $rk[i]$ 此时代表 $s[i,\min(n,i + w - 1)]$ 在 ${s[i,\min(n,i+w-1]|i \in [1,n]}$ 中的排名。

以 $rk[i]$ 为第一关键字， $rk[i + w]$ 为第二关键字，就可以求出长度为 $2w$ 的字符串的 $rk$ 数组。
特别地，若 $i + w > n$ 则令其为无穷小。

倍增排序示意图：

如果使用常规的基于比较的排序算法，可以做到 $O(n \log^2 n)$ 的复杂度。

而由于 $rk[i]$ 与 $n$ 同阶，往往可以采用基数排序来做到 $O(n)$ 单次排序，从而优化到 $O(n \log n)$ 的复杂度。

这里先给出基于 sort 的方法，便于理解：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


#include <cstdio>  
#include <algorithm>  
#include <cstring>  
const int maxn = 1e6 + 100;  
char s[maxn];  
int n, w, sa[maxn], rk[maxn << 1], oldrk[maxn << 1];  
bool cmp(int a, int b)  
{  
    if (rk[a] != rk[b]) return rk[a] < rk[b];  
    return rk[a + w] < rk[b + w];  
}  
int main()  
{  
    scanf("%s", s + 1);  
    n = strlen(s + 1);  
    for (int i = 1; i <= n; ++i) sa[i] = i, rk[i] = s[i];  
    for (w = 1; w < n; w <<= 1)  
    {  
        std::sort(sa + 1, sa + 1 + n, cmp);  
        for (int i = 1; i <= n; ++i) oldrk[i] = rk[i];  //过程中需要用到原排名，因此拷贝一份  
        for (int i = 1, p = 0; i <= n; ++i)  
        {  
            if (oldrk[sa[i]] == oldrk[sa[i - 1]] && oldrk[sa[i] + w] == oldrk[sa[i - 1] + w])  
                rk[sa[i]] = p;  //若两个子串相同，其排名需要相同  
            else rk[sa[i]] = ++p;  
        }  
    }  
    for (int i = 1; i <= n; ++i) printf("%d ", sa[i]);  
    return 0;  
}  

倍增基数排序

现在我们考虑如何使用基数排序进行优化。

其实就是朴素的基数排序，但为了减小常数，有如下的黑科技：

第二关键字无需计数排序。第一关键字相同时，先将 $i + w > n$ 的即第二关键字无穷小的元素放入队列中，再将普通元素放入。
优化计数排序的值域。每次对 $rk$ 数组进行了去重，因此可以不断缩小计数的值域。
用函数 $cmp$ 来计算是否重复，优化缓存。

我们约定：

$sa[i]$ 表示排名第 $i$ 的后缀。
$rk[i]$ 表示后缀 $i$ 的排名。
$tp[i]$ 表示第二关键字排名为 $i$ 的后缀。
$tax$ 为辅助基数排序所用的桶。
$m$ 为当前计数排序的值域。

先来看基数排序部分：

1
2
3
4
5
6
7


void RadixSort()  
{  
    for (int i = 1; i <= n; ++i) tax[i] = 0;  
    for (int i = 1; i <= n; ++i) tax[rk[i]]++;          //统计第一关键字排名为 i 的有多少个  
    for (int i = 1; i <= m; ++i) tax[i] += tax[i - 1];  //做前缀和方便得到全局排名  
    for (int i = n; i; --i) sa[tax[tp[i]]--] = tp[i];   //倒序遍历，保证在第一关键字相同的中，第二关键字靠后的排名靠后  
}  

这里还是比较容易理解的，先预处理出 $tp$ 数组，然后开一个桶。

对于第一关键字相同的，通过桶来分配排名。

那么主体部分跟之前大概一致。
只是多了处理第二关键字序列 $tp$ 的环节。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


#include <cstdio>  
#include <algorithm>  
#include <cstring>  
const int maxn = 1e6 + 100;  
char s[maxn];  
int n, M, sa[maxn], rk[maxn << 1], oldrk[maxn << 1], tax[maxn], tp[maxn];  
void RadixSort()  
{  
    for (int i = 1; i <= M; ++i) tax[i] = 0;  
    for (int i = 1; i <= n; ++i) tax[rk[i]]++;          //统计第一关键字排名为 i 的有多少个  
    for (int i = 1; i <= M; ++i) tax[i] += tax[i - 1];  //做前缀和方便得到全局排名  
    for (int i = n; i; --i) sa[tax[rk[tp[i]]]--] = tp[i];  //倒序遍历，保证在第一关键字相同的中，第二关键字靠后的排名靠后  
}  
inline bool same(int a, int b, int w) { return oldrk[a] == oldrk[b] && oldrk[a + w] == oldrk[b + w]; }  
void SuffixArray()  
{  
    M = 300;  
    for (int i = 1; i <= n; ++i) rk[i] = s[i], tp[i] = i;  
    RadixSort();  
    for (int w = 1, p; p < n; w <<= 1, M = p)  //reset count range  
    {  
        p = 0;  
        for (int i = n - w + 1; i <= n; ++i) tp[++p] = i;  //第二关键字为无穷小的先放入  
        for (int i = 1; i <= n; ++i) if (sa[i] > w) tp[++p] = sa[i] - w;  //初始化第二关键字  
        RadixSort();  
        for (int i = 1; i <= n; ++i) oldrk[i] = rk[i];  
        p = 0;  
        for (int i = 1; i <= n; ++i) if (same(sa[i - 1], sa[i], w)) rk[sa[i]] = p; else rk[sa[i]] = ++p;  
    }  
}  
int main()  
{  
    scanf("%s", s + 1);  
    n = strlen(s + 1);  
    SuffixArray();  
    for (int i = 1; i <= n; ++i) printf("%d ", sa[i]);  
    return 0;  
}  

$O(n)$ 求法

在一般题目中，常数较小的倍增完全够用了。
但的确还有 $O(n)$ 的求法：

SA-IS
DC3

后缀数组的应用

寻找最小的循环移动位置

{{{
给出一个环字符串 $s$ ，从任意点出发可以得到一个字符串 $t$ ，对所有可能的 $t$ 进行排序。

破环为链，将字符串 $s$ 复制一份之后，就成了后缀排序问题。我们只需要排序前 $|s|$ 位即可，可以发现对后面的位排序是没有影响的。

为什么没有影响？因为 $|s|$ 位后又开始了循环，如果有不同则在之前已经被分出大小了。

}}}

代码看：“这里”

在字符串中找子串

在原串 $S$ 中在线匹配模式串 $T$ .

如果可以离线，那么"AC 自动机"是一种优秀的解决方案。
而对于在线匹配，可以用后缀数组实现，单个模式串时间复杂度为 $O(|T| \log |S|)$ .

我们先构造出 $S$ 的后缀数组，然后查找子串 $T$ .
如果 $T$ 在 $S$ 中出现过，那么 $T$ 一定是 $S$ 的某个后缀的前缀。
求出 $sa$ 数组后，我们二分 $T$ 对应的后缀，用 $O(|T|)$ 的时间复杂度进行比较。
总复杂度即 $O(|T| \log |S|)$ .

这种方法还可以拓展到求模式串的出现次数，同样用二分解决。
而输出每次出现的位置也很轻松，即对应的 $sa[i]$ 为起点。

从字符串首尾取字符最小化字典序

{{{
给你一个字符串，每次从首或尾取走一个字符，问能够组成的字符串中字典序最小的一个。

考虑依次判断当前头尾字符应该取哪一个。
如果头尾字符不同，那么显然可以直接贪心取小的。
如果头尾字符相同，事情变得棘手起来。

事实上，我们可以比较当前首字符开始的后缀与尾字符开始的前缀的字典序，然后贪心地取。
感性理解一下。

问题就只剩下了求首字符开始的后缀与尾字符开始的前缀的字典序大小关系。
考虑使用后缀排序，将原串和反串放在同一个字符串里，在 $i + 1$ 位置处用某个分隔符隔开。
这样，对于位置 $ i $ ，其后缀的排名为 $ rk[i] $ ，其前缀的排名为 $ rk[2n - i + 2]$ .

}}}

“例题”

height 数组

LCP（最长公共前缀）

最长公共前缀，顾名思义。

两个字符串 $S$ 与 $T$ 的 LCP 就是最大的 $x$ 满足 $S_i = T_i (\forall i \in [1,x])$ .

下文以 $\operatorname{lcp}(i,j)$ 表示后缀 $i$ 与后缀 $j$ 的最长公共前缀长度。

height 数组定义

$height[i] = \operatorname{lcp}(sa[i-1],sa[i])$ .

具体地， $height[i]$ 即第 $i$ 名的后缀与它的前一名的后缀的最长公共前缀长度。

为了方便，我们记： $h[i] = height[rk[i]]$ .
即 $h[i]$ 对应位置 $i$ 的后缀的 $height$ 值。

$height[1]$ 可以视为 $0$ .

$O(n)$ 求 height 数组需要的一个引理

$$ h[i] \ge h[i-1] - 1 $$

这乍一看是不怎么显然的。我们猜测这也用到了字符串的公共部分带来的性质。

证明：

首先有一个证明需要用到的引理。
后缀 $i$ 和后缀 $j$ 的最长公共前缀长度为： $\min {height[k] \mid rk[i] \le k \le rk[j]}$ .
先感性理解有，由于按字典序排序，那么字典序排名相差越大，相似度越低。
然后再感性理解有， $height$ 数组具有传递性，一路传递下来，不断缩紧限制，那么就是取最小值了。
具体证明可以看下面的"两子串最长公共前缀"部分。

当 $h[i-1] - 1 = 0$ 时，即 $h[i-1] = 1$ 时，显然成立。

当 $h[i-1] > 1$ 时：
设后缀 $i-1$ 为 aAD，其中 A 是一个长度为 $h[i-1] - 1$ 的字符串，a 是一个字符，D 是可空字符串。
那么后缀 $i$ 就是 AD，即向后一位舍去首位字符。

回顾一下 $height$ 数组的定义，写出：

$$ \begin{aligned} & h[i] = \operatorname{lcp}(sa[rk[i] - 1],sa[rk[i]])\\ & h[i-1] = \operatorname{lcp}(sa[rk[i-1] - 1],sa[rk[i-1]) \\ \end{aligned} $$

设 $sa[rk[i-1]-1]$ 是 aAB，其字典序小于后缀 $i-1$ ，且与后缀 $i-1$ 的最长公共前缀为 aA.
也就是说， $\operatorname{lcp}(i,sa[rk[i-1]-1]) = aA$ .

接着， $sa[rk[i-1]-1] + 1$ 是 AB，即后移了一位。

可以发现，AB 的字典序一定小于 AD，我们通过将后缀 $i-1$ 对应的 $sa[rk[i-1] - 1]$ 的字符串右移一位对齐，而利用后缀 $i-1$ 与后缀 $i$ 的公共部分得到了相对关系。

那么： $sa[rk[i-1]-1] + 1$ 的字典序小于 $sa[rk[i]]$ 的字典序。

根据之前的引理：
$\operatorname{lcp}(sa[rk[i-1]-1]+1,sa[rk[i]]) = \min {height[k] \mid rk[sa[i-1]-1]+1 \le k \le rk[i]}$
当 $k=rk[ii]$ 时，就能得到：
$\operatorname{lcp}(sa[rk[i-1]-1]+1,sa[rk[i]]) \le h[i]$

而我们知道， $sa[rk[i-1]-1]+1$ 是 AB，后缀 $i$ 是 AD，而 A 是一个长度为 $h[i-1]-1$ 的字符串。

那么原命题就得证了：

$$ h[i] \ge h[i-1] - 1 $$

$O(n)$ 求 height 数组的代码实现

又是均摊复杂度的代码。

1
2
3
4
5
6
7
8
9


void initHeight()  
{  
    for (int i = 1, k = 0; i <= n; ++i)  
    {  
        if (k) --k;  
        while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;  
        height[rk[i]] = h[i] = k;  
    }  
}  

不难发现， $k$ 在每一位最多减少 $1$ ，而 $k$ 的上限是 $n$ ，那么：
$k$ 最多减少 $n$ 次，最多加 $2n$ 次。
时间复杂度 $O(n)$ .

height 数组的应用

在 $height$ 数组的应用中，最重要的思想是：

子串是后缀的前缀。

两子串最长公共前缀

$$ \operatorname{lcp}(sa[i],sa[j]) = \min {height[i,\ldots,j]} $$

感性理解在"上文"中已经提及，这里直接引用：

首先有一个证明需要用到的引理。
后缀 $i$ 和后缀 $j$ 的最长公共前缀长度为： $\min {height[k] \mid rk[i] \le k \le rk[j]}$ .
先感性理解有，由于按字典序排序，那么字典序排名相差越大，相似度越低。
然后再感性理解有， $height$ 数组具有传递性，一路传递下来，不断缩紧限制，那么就是取最小值了。
具体证明可以看下面的((20210120133815-ni7e3if “{{.text}}”))部分。

严谨证明可以看：徐智磊的论文

有了这个定理，两子串最长公共前缀，就可以转化为 RMQ 问题。

比较两子串的大小关系

需要比较 $A = S[a..b]$ 和 $B = S[c..d]$ 的大小关系。

若 $\operatorname{lcp}(a,c) \ge \min(|A|,|B|)$ ，则 $A < B \iff |A| < |B|$ .
否则， $A < B \iff rk[a] < rk[c]$ .

不同子串的数目

子串就是后缀的前缀。

不难得知，一个字符串的子串总数是 $\dfrac{n(n+1)}{2}$ ，我们只需要减去重复的子串的数目。

如果按照字典序顺序枚举后缀，每次新增的子串，就是除去已经在上一个后缀中出现过的前缀之外的前缀，也就是除了公共前缀外的前缀。
那么重复的子串数目，就是与上一个后缀的公共前缀数目，即 $height[i]$ .

$$ \dfrac{n(n+1)}{2} - \sum \limits _{i=2}^n height[i] $$

例题：“洛谷 P2408 不同子串个数”

出现至少 $k$ 次的子串的最大长度

在原串中出现至少 $k$ 次的子串的最大长度。

让我们思考，子串就是后缀的前缀，而公共前缀的最长长度我们是可以求出的。
问题转化为在 $height$ 数组上连续 $k-1$ 个数的最小值的最大值，滑动窗口求解即可。